中学生が苦手な図形を克服するためのポイントを説明 |

※この記事には一部PRが含まれます。

塾オンラインドットコム「合格ブログ」です。

小学生と中学生向けに、勉強に役立つ情報を発信している教育メディアです。

今回のお悩みはこちら。

相談者

図形が苦手？

勉強法を知りたい

公式っていくつあるの？

中学生が苦手な図形を克服するヒントについて説明します。

先生

中学生の苦手な図形を克服したいですよね？

今回紹介する「中学生が苦手な図形を克服するためのポイントを説明」を読めば、苦手な図形を克服できるはずです。

この記事では、図形の苦手を克服するための具体的な勉強法を紹介しています。

読み終えると、図形の苦手が克服できるヒントになるはず。

また、最後にいろいろな数学の勉強法を紹介しているので、参考にしてください。

もし、短期間で図形の苦手を克服するのであれば、東大生と東大院生の指導が受けられる！「トウコベ：東大生のオンライン個別指導」がおすすめです。

東大生と東大院生から教えてもらえると高額のイメージがありますが、低料金で高品質の授業が受けられます。

オンライン個別指導：トウコベの公式ホームページをチェック！

読み終えるとわかること

中学生が図形の苦手を克服するヒント。

中学生の図形勉強法。

中学生「図形の公式」。

図形の苦手を克服する！おすすめタブレット教材の紹介

おすすめ塾

講師のほとんどが東大・東大院生

オンライン個別指導の「トウコベ」

しかも、圧倒的低価格を実現した！

オンライン個別指導

部活が忙しい生徒にも対応！

自宅で勉強できるから、集中力UP！

成績アップの近道！

30日間の返金保証制度も安心！

トウコベをもっと詳しく

＼トウコベの資料をダウンロード／
↓↓↓
トウコベの公式HPをチェック！

関連記事

【トウコベ】口コミ・評判を徹底解説！知っておきたい口コミの真実

トウコベの料金（入会金・月謝）は高い？他のオンライン塾と徹底比較！

Contents

1 中学生が苦手な図形を克服するためのポイントを説明
2 図形の勉強法を知って苦手克服
3 図形の性質を知って苦手克服
4 タブレット学習教材が中学生におすすめな理由
5 まとめ：中学生が苦手な図形を克服するためのポイントを説明
- 5.1 まとめ：中学生が苦手な図形を克服するためのポイント
- 5.2 中学生の数学に関する記事

中学生が苦手な図形を克服するためのポイントを説明

先生

中学生が図形を嫌いになる理由についてまとめてみました。

以下のポイントについて説明しています。

図形が苦手なぜ？中学生が図形を苦手になる理由
中学生で習う図形とは
空間図形が難しい理由は何ですか？
塾で苦手を克服する

図形が苦手なぜ？中学生が図形を苦手になる理由

中学生はなぜ図形が苦手になるのでしょうか？

図形と言っても、大きく分けて平面図形と空間図形の2種類があります。

平面図形が苦手な生徒の理由は、「平行や直線などの用語や図形の性質を理解していない」からです。

また、空間図形が苦手な生徒の理由は、「立体を頭の中にイメージできない」からです。

特に空間図形の問題を解くためには、立体を回転させたり、裏返したり、切ってみたりと、さまざまな方法で頭の中で動かす必要があります。

最初はこれが意外に難しくて、図形につまずく中学生が多いのです。

中学生の図形が苦手な場合は、苦手な理由を追求してから図形の苦手を克服するのがおすすめです。

中学生で習う図形とは

中学生の数学において、苦手な単元を学年別に整理すると、以下のようになります。

・数と式

・図形

・関数

・その他

図形と関数は中学生が苦手な単元です。

中学生で学習する図形の単元を学年別に整理すると、以下のようになります。

中学1年生	平面図形「直線と角・移動・作図・おうぎ形など」、空間図形「位置関係・展開図・表面積・体積・球」
中学2年生	合同「合同・証明など」、三角形と四角形「二等辺三角形・直角三角形・平行四辺形」
中学3年生	相似「相似・証明・平行線と線分比・面積比・体積比」、三平方の定理「三平方の定理・平面、空間図形」

表を見てもわかる通り、中学1年生で学習する内容が発展した内容を中学2年生で学習し、さらに応用したものを中学3年生で学習する仕組みです。

つまり、中学1年生の図形の内容を理解していないと、中学2年生、中学3年生になっても図形を理解することは難しくなるのです。

すなわち、図形の苦手は早めに克服しないと大変なことになるのです。

参考記事：中学生の数学が全くできないと悩む親へ！原因と今すぐ試せる解決策！

空間図形が難しい理由は何ですか？

中学生にとって空間図形は難しいと感じやすい科目です。

その理由は、

想像力が求められる
多角的な視点が必要
経験不足
苦手意識

などが挙げられます。

克服するには、

図形を実際に描く
様々な角度から図形を見る
問題を丁寧に解く
繰り返し練習する
わからないことは先生や友達に聞く
苦手意識を持たない

ことが大切です。

空間図形は理解すれば非常に役に立つものです。

諦めずに、積極的に学習に取り組みましょう！

塾で図形の苦手を克服する

中学生の生徒の中には、計算はできるけど図形が苦手。または、図形で数学が苦手になったという生徒がたまにいます。

中学生の数学ではどの学年も図形に関する問題があり、特に中学2年生から学習する「図形の証明」は図形の知識と文章力が求められる分野となります。

入試においても証明問題が苦手となり得点が取れないという単元でもあります。

塾によっては、図形を得意科目にするために授業中のノートのとり方から問題の解き方まで丁寧に指導しています。

また、数学専門の塾もあるため、図形を効率よくマスターできるでしょう。

数学に強いオンライン塾

森塾のオンライン部門！オンライン個別指導生徒数No.1のそら塾
※保護者が選ぶオンライン学習塾NO.1を獲得！しかも低料金！

東大生によるオンライン個別指導トウコベ
※講師は全員東大生・東大院生！最高レベルの授業がこの価格で実現！

圧倒的な合格実績！オンラインプロ教師のメガスタ！
※全国に40,000人の講師が在籍！きっとあなたにピッタリの講師が見つかる！

参考記事：【メガスタ】料金は高い？他のオンライン家庭教師と料金を比較調査

図形の勉強法を知って苦手克服

先生

図形の勉強法についてまとめてみました。

以下のポイントについて説明しています。

小学生の図形の復習
図を書けるように練習する
図形の性質を覚える

小学生の図形の復習

図形問題が得意な生徒は、小学生の頃からノートに図形を書いたり、実際に切ったり組み立てたりして図形を理解しています。

この習慣が小学生の時にできていない生徒は、基本的なことを確認する上で、小学生の図形を復習するのがおすすめ。

なぜなら、小学生で学習した延長が中学生で学習する図形だからです。

小学生の図形をしっかりと復習して、理解できない場合は、繰り返し基本事項を確認してください。

小学生の図形を復習することは決して遠回りではありません。

参考記事：算数と数学の違いを簡単に”超”わかりやすく解説【たった1分で解決！】

是非、試してみてください。

図形問題の図を書けるように練習。

図形問題が苦手な中学生の場合、自分でノートに実際に図形を書いてみる練習をすることが大切。

理由は、図形を理解する上で、図形の定理や定義、角度や長さの求め方などを、自分でノートに書いた図の上に書き込んで、確認して理解することで学力として身につくからです。

応用問題を解く場合には、図形を分解した図を書いたり、立体を平面に書き直したりすることで、定規を使わなくても図形が書けるようになると安心です。

同じ問題を繰り返し解いて練習することで身につけられるでしょう。

参考記事：【中学生の国語】定期テスト対策！前日でも間に合う！点数をUPする勉強法（現代文・古文・漢字別）

図形の性質を覚える

定義と定理の意味を理解する。

「定義」とは、用語の意味をはっきり述べたもので、基本的には1つの用語に対して1つの説明しかありません。

それに対して、定義から導かれたものもしくは証明された事柄を「性質」や「定理」といいます。

これは1つとは限りません。いろいろな「性質」の中でよく使われるものを特に「定理」とよんでいます。

例えば

二等辺三角形の性質を聞かれた場合の答えとして、

「２つの辺の長さが等しい三角形」

「２つの角の大きさが等しい三角形」

「ひし形を対角線で切った一方の三角形」

どれも正解ですが、

「二等辺三角形とは、２つの辺の長さが等しい三角形」のように、言葉の意味をはっきりと述べたものを、定義する。

一方、「二等辺三角形の２つの角の大きさは等しい」・「二等辺三角形の頂角の二等分線は、底辺を垂直に二等分する」のように、定義をもとに証明された大切なものを定理と言います。

つまり、「二等辺三角形とは２つの辺の長さが等しい三角形」（定義）をもとにして、「二等辺三角形の２つの角の大きさは等しい」（定理）を証明できるのです。

しっかりと言葉の意味と図形の性質を理解するのが図形を克服するポイント。

オンライン家庭教師

塾より成績が上がる！オンライン家庭教師のWAM
※難関大学の講師が親切丁寧に指導！忙しい生徒にピッタリ！

短期間で成績向上！オンライン家庭教師：マナリンク
※動画でプロの講師が選べる画期的なシステム

リーズナブルな料金設定！オンライン家庭教師銀河
※中学生：1コマ30分：1,375円〜！お得に選ぶなら！銀河！

図形の性質を知って苦手克服

先生

図形の性質の公式についてまとめてみました。

以下のポイントについて説明しています。

二等辺三角形の性質
平行四辺形の性質
正三角形の性質
合同相似条件

私が実践していた図形の勉強の仕方を少しご説明いたします。

まずは、以下の代表的な公式をとにかく覚える。

これだけで図形の理解は高まります。

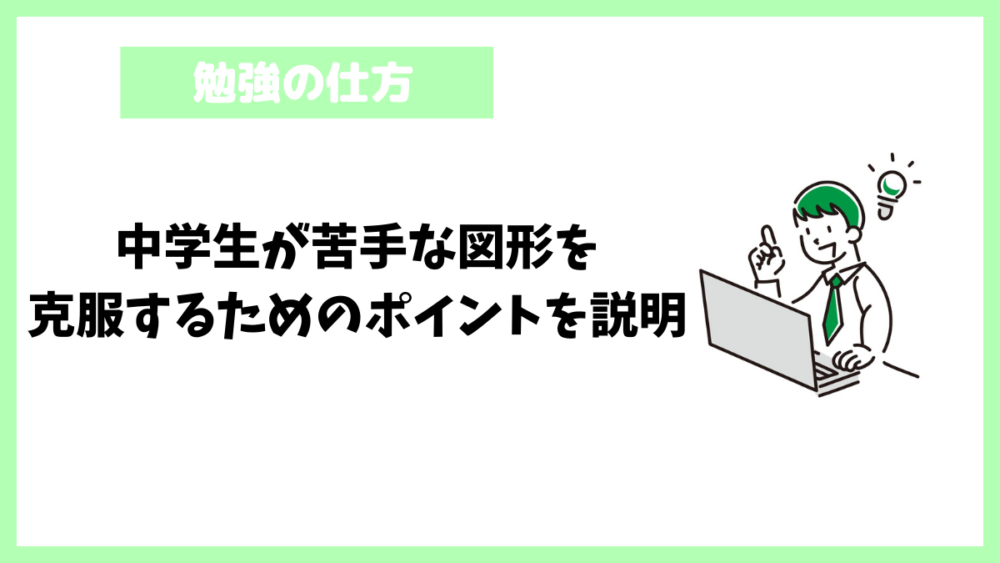
二等辺三角形

底角が等しい。

頂角を二等分する線分は底辺を垂直に二等分する。

また「2辺が等しい」もしくは「2つの角が等しい」という条件を持つ三角形は二等辺三角形になる。

参考記事：中学生の因数分解！やり方をわかりやすく解説（公式・計算方法・たすきがけ）

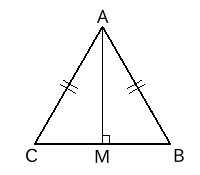
平行四辺形

2組の対辺がそれぞれ平行。

2組の対辺がどちらも等しい。

2組の対角がどちらも等しい。

対角線がそれぞれの中点で交差。

1組の対辺が平行かつその長さが等しい。

長方形・ひし形・正方形も平行四辺形の一種ですが、それぞれの定義は以下の通りとなります。

長方形：4つの角が全て直角な四角形。

ひし形：4つの辺が全て等しい四角形。

正方形：4つの角が全て直角かつ4つの辺が全て等しい四角形。

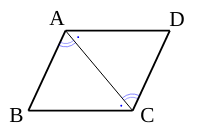
正三角形

3辺が全て等しい。

3つの角が全て60度。

合同相似条件

合同・相似条件
＜三角形の合同条件＞	3辺がそれぞれ等しい 2辺とその間の角が等しい 1辺とその両端の角が等しい
＜直角三角形の合同条件＞	斜辺とその他の1辺が等しい斜辺と1つの鋭角が等しい
＜三角形の相似条件＞	3辺の比がそれぞれ等しい 2辺の比とその間の角が等しい 2組の角が等しい

タブレット学習教材が中学生におすすめな理由

勉強が嫌いな中学生は、タブレット学習教材で勉強するのも良い方法。

なぜなら、タブレット学習教材を利用することで、ゲーム感覚で集中して学習できるからです。

タブレット学習教材には、学校の授業内容を予習・復習できるものや、苦手な分野を克服するためのものなど、さまざまな種類があります。

また、子どもの年齢や学習レベルに合わせて選べるため、子ども一人ひとりに合った学習ができます。

タブレット学習教材は、子どもたちがゲーム感覚で学習できるので、勉強が苦手な子どもでも楽しく学習できるでしょう。

また、タブレット学習教材には、子どもの学習状況を保護者が確認できる機能が付いているものもあるので、子どもの学習進捗を把握できます。

以下は、中学生向けのタブレット学習教材のおすすめポイント。

・学校の授業内容を予習・復習できる

・苦手な分野を克服できる

・子どもの年齢や学習レベルに合わせて選べる

・子どもたちがゲーム感覚で学習できる

・保護者が子どもの学習状況を確認できる

タブレット学習教材は、勉強が嫌いな中学生、学校の授業に遅れを取っている中学生や、勉強が苦手な中学生にもおすすめです。

タブレット学習教材が中学生におすすめな理由

中学生の図形の勉強におすすめタブレット学習教材比較表

タブレット学習教材名	月謝	特徴
進研ゼミ：中学講座	中学1年生：6,400円〜	ベネッセが提供している、タブレット学習教材。中学生の利用者数No.1。
すらら	小中コース 8,000円〜	AI×アダプティブラーニング「すらら」、マナブをサポートする最先端学習システム。小学生から高校生まで、国・数・理・社・英の5教科を学習できるICT教材
スマイルゼミ	7,480円〜	「まなぶ」「みまもる」「たのしむ」の3つのバランスを大切にして、勉強したい気持ちを逃さない。
デキタス	5,280円〜	勉強嫌いでも、勉強が習慣化できる！おすすめのタブレット学習教材

※オンライン料金の詳細については公式サイトからお問い合わせください。※社名をタップすると公式ホームページに移動します。
※学年や講師ランク・授業時間により料金は変動します。※自社調べ（税込）

進研ゼミ：中学講座は中学生におすすめの教材

中学生利用者NO.1！進研ゼミ：中学講座の基本情報

月謝	【月謝例】中学1年生：6,400円〜中学2年生：6,570円〜中学3年生：7,090円〜
対応科目・コース	国語、数学、理科、社会、英語
学習機能	教科書対応のテキストで、予習も復習もバッチリ！お使いの教科書に合わせたテキストなので、予習はもちろん復習にも効率的に
管理機能	AIのレッスン提案で迷わない実力に合わせて学習スタート学習達成後のごほうびでやる気が続く
サポート体制	月1回、赤ペン先生がお子さま一人ひとりを添削し、丁寧に指導。担任制なので、毎回同じ先生に提出する楽しみがうまれ、毎月の学習の仕上げとしてしっかり取り組めます。

進研ゼミ中学講座の特徴

進研ゼミ中学講座は、ベネッセコーポレーションが提供している中学生向けの通信教育です。

1969年にスタートして以来、多くの中学生に利用されてきました。進研ゼミ中学講座の特徴は、以下の通りです。

学校の授業内容に沿った教材で、予習・復習が効率的にできる。
タブレット学習を利用することで、ゲーム感覚で学習できます。
赤ペン先生による添削指導で、記述力や思考力を鍛えられる。
応用問題や演習問題で、実力を身につけられる。
夏休み特訓や冬期講習など、季節ごとの特別講座が充実。
保護者向けのサポートサイトがあり、子どもの学習状況を把握できます。

進研ゼミ中学講座は、中学校の授業内容をしっかり学びたい、記述力や思考力を鍛えたい、夏休みや冬休みの学習を充実させたい、といった中学生におすすめです。

＼中学生の利用者NO.1の通信教育／
安心して利用できる
↓↓↓

進研ゼミ中学講座

すらら：無学年方式で図形の勉強ができるオンライン教材

「すらら」の基本情報

受講費用の安さ	■入会金・小中・中高5教科コース：7,700円・小中・中高3教科、小学4教科コース：11,000円 ■3教科（国・数・英）コースの月謝例・小中コース月額：8,800円〜小学1年生～中学3年生までの3教科（国・数・英）の範囲が学び放題・中高コース月額：8,800円〜
対応科目・コース	4教科（国・数・理・社）コース 5教科（国・数・理・社・英）コース無学年方式で中学英語も先取り学習できる
学習機能	キャラクターによるレクチャーからドリル機能が充実「すらら」は読み解くだけではなく、見て、聞いて学べる
管理機能	「すらら」はAI搭載型ドリルだから自分のつまずきポイントがわかる！
サポート体制	学習習慣の身に付け方を始めとした学習に関する悩みや、基礎学力、成績を上げるための学習設計をサポートします。

すららの特徴

すららは、株式会社すららネットが提供している中学生向けのオンライン学習教材です。

2010年にスタートして以来、多くの中学生に利用されてきました。

すららの特徴は、以下の通りです。

学年にとらわれない無学年方式で、子どものペースに合わせて学習できます。
子どもの弱点をAIが自動診断し、苦手な分野を効率的に克服できます。
ゲーム感覚で学習できるので、勉強が苦手な子どもでも楽しく学習できます。
保護者向けのサポートサイトがあり、子どもの学習状況を把握できます。

すららは、学習に苦手意識を持っている子どもや、効率的に学習を進めたい子どもにおすすめです。

当サイトで人気No.1の通信教材！
是非！すららを選択肢の一つに
↓↓↓

すらら

スマイルゼミ：最適な学びが継続するタブレット教材

スマイルゼミの基本情報

お手軽な受講費用	【中学1年生】月謝例＜標準クラス＞・7,480円〜：12か月一括払い/月あたり
対応科目・コース	国語・数学・理科・社会はもちろんのこと、英語やプログラミングも1年生から学習できる
学習機能	アニメーションによる解説で公式の持つ意味を正しく理解できる手をついて書ける学習専用タブレットを使用
管理機能	スマイルゼミのタブレットは、利用時間を「1日〇時間」という形で制限可能
サポート体制	全額返金保証制度あり

スマイルゼミの特徴

スマイルゼミは、ジャストシステムが提供している中学生向けのタブレット学習教材。

2012年にスタートして以来、多くの中学生に利用されてきました。

スマイルゼミの特徴は、以下の通りです。

タブレット端末を使って学習できるので、ゲーム感覚で楽しく学べます。
子どもの学習状況をAIが分析して、一人ひとりに合った学習内容を自動的に提案してくれます。
保護者向けのサポートサイトがあり、子どもの学習状況を把握できます。

スマイルゼミは、タブレットで最適な学習を継続させたい人におすすめです。

中学生の学びが継続するタブレット
＼返金保証制度あり／
↓↓↓

スマイルゼミ

中学生に最適なタブレット教材：デキタス

中学生におすすめ！デキタスの基本情報

項目	デキタスの公式サイト
受講費用	中学生：5,280円〜
対応科目・コース	国語、数学、英語、理科、地理、歴史、公民、国文法、英語検定
学習機能	ポップなキャラクター＆わくわくする授業！
管理機能	テストモード搭載
サポート体制	学習結果は表・グラフ・カレンダー等でひと目で確認することができます。
無料体験の有無	無料体験実施中