
「※この記事には一部PRが含まれます」
「文字式の計算が始まったけど、分配法則ってなんだか難しそう…」「括弧の前のマイナスで、いつも符号を間違えちゃう…」
中学1年生の数学で登場する「分配法則」。
これは、これから学ぶ方程式や関数でもずっと使い続ける、数学の超重要ルールです。
この記事では、そんな分配法則の基本から、テストで差がつく応用問題まで、たくさんの練習問題を用意しました。
つまずきやすいポイントも、イラストや丁寧な解説でしっかりサポートします。
この記事を読めば、あなたは分配法則の計算に自信がつき、文字式の問題がスラスラ解けるようになります。
一緒に文字式をマスターしていきましょう!
記事のポイント
図解と例題で本質から理解する分配法則
レベル別練習問題で計算力を徹底強化
ミスしやすいポイントと具体的な対策を解説
練習問題で自宅学習を強力にサポート
東大生家庭教師
現役の東大生が指導するオンライン家庭教師!
当サイト人気ランキングTOP3
第1位:東大生によるオンライン個別指導トウコベ
※講師のほとんどが現役東大生!しかも、圧倒的な低価格を実現!安心の返金保証制度で生徒の成績アップをサポートします。
第2位:オンライン家庭教師「東大先生」
※当サイトで人気の東大生によるオンライン家庭教師!講師全員が現役東大生・東大院生!資料請求で勉強が変わること間違いなし!
第3位:オンライン東大家庭教師友の会
※東大生をはじめとする難関大生がマンツーマンでオンライン指導!講師の2人に一人が厳しい採用基準を突破した現役東大生!
Contents
分配法則とは?イラストでわか文字式の基本公式

まずは「分配法則ってそもそも何?」というところからおさらいしましょう。
分配法則の目的は、括弧(かっこ)を外して式を計算しやすくすることです。
言葉だけだと難しく感じるかもしれませんが、仕組みはとてもシンプルです。
- 分配法則の2つの公式
- 面積図で理解する分配法則の仕組み
- 計算ミスを防ぐ3つのステップ
分配法則の2つの公式
分配法則には、2つの基本的な形があります。
- a(b + c) = ab + ac
- (a + b)c = ac + bc
簡単に言うと、「分配法則とは、括弧の外にある数や文字を、括弧の中のすべての項に、それぞれ公平に掛け算する」というルールです。
a(b + c) という式なら、外にある a を、中の b と c の両方に掛けてあげるイメージです。

参考記事:中学生の因数分解!やり方をわかりやすく解説(公式・計算方法・たすきがけ)
面積図で理解する分配法則の仕組み
「どうしてそんなルールになるの?」と疑問に思った人のために、長方形の面積で考えてみましょう。
下の図を見てください。
大きな長方形全体の面積は「縦 × 横」なので a × (b + c) と表せます。
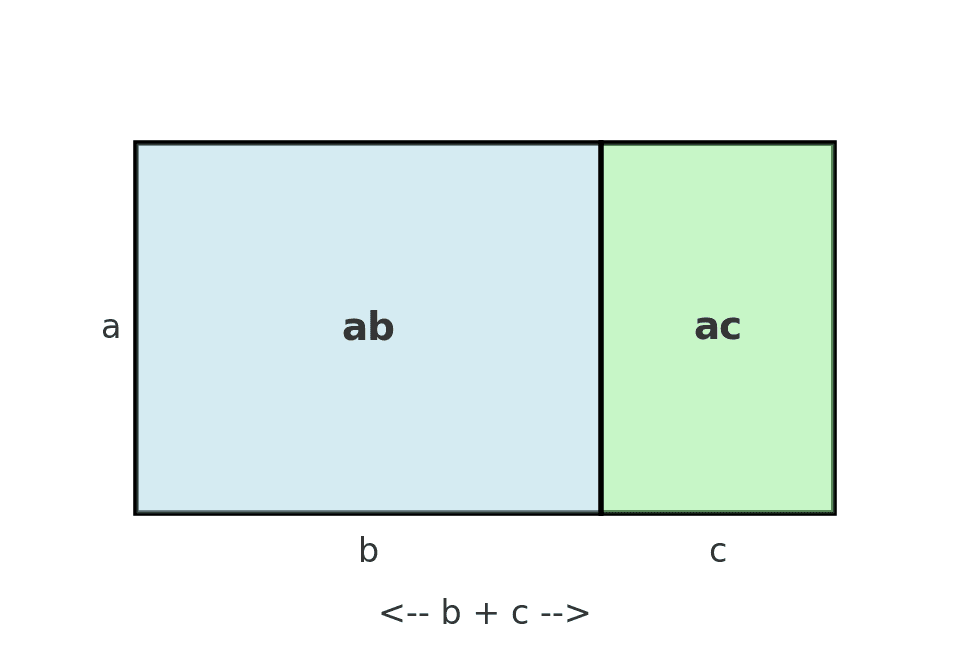
この大きな長方形は、2つの小さな長方形(面積 ab と面積 ac)を合わせたものとも考えられます。
つまり、全体の面積は ab + ac とも表せます。
このことから、a(b + c) と ab + ac は等しいということが分かります。
これが分配法則の正体です。
計算ミスを防ぐ3つのステップ
分配法則の計算を正確に行うには、以下の3ステップを意識するのがおすすめです。
- 掛ける数と掛けられる項を確認
括弧の外にある数(文字)と、括弧の中にある項をすべて確認します。 - 矢印でつなぐ
計算ミスを防ぐために、どの項に掛けるのかを矢印で書いておくと効果的です。特に、括弧の中に項が3つ以上ある場合や、複雑な式で役立ちます。 - 順番に計算する
矢印に沿って、符号に注意しながら一つひとつ丁寧に掛け算し、式を完成させます。
おすすめ塾
講師のほとんどが東大・東大院生
東大生が指導する塾としてはコスパが良い
オンライン個別指導
部活が忙しい生徒にも対応!
自宅で勉強できるから、集中力UP!
成績アップの近道!
30日間の返金保証制度も安心!

\トウコベの資料をダウンロード/
↓↓↓
トウコベの公式HPをチェック!
関連記事;トウコベの料金は高い?小中高の月謝総額と他塾比較【料金表】
レベル別!分配法則の練習問題

それでは、実際に問題を解いて分配法則に慣れていきましょう。
基礎から順番にチャレンジしてみてください。
各問題の下に詳しい解答と解説があります。
- 【基礎】基本的な文字式の計算問題
- 【頻出】括弧の前にマイナスがある問題
- 【苦手克服】分数・小数を含む計算問題
【基礎】基本的な文字式の計算問題
まずは、分配法則の基本となる問題です。
符号に注意して解いてみましょう。
問題1
3(x + 5)
解答・解説
括弧の外にある 3 を、中の x と +5 の両方に掛けます。
3 × x = 3x
3 × (+5) = +15
よって、答えは 3x + 15 となります。
問題2
5(2a - 4)
解答・解説
5 を 2a と -4 の両方に掛けます。
5 × 2a = 10a
5 × (-4) = -20
よって、答えは 10a - 20 となります。

【頻出】括弧の前にマイナスがある問題
括弧の前にマイナスがある場合は、特に符号ミスが起こりやすいポイントです。
慎重に計算しましょう。
問題1
-(y - 7)
解答・解説
括弧の前の - は、-1 が隠れていると考えるのがコツです。
つまり、-1 を y と -7 の両方に掛けます。
(-1) × y = -y
(-1) × (-7) = +7
よって、答えは -y + 7 となります。
括弧の中の符号がすべて逆になると覚えておきましょう。
問題2
-4(2x - 3)
解答・解説
-4 を 2x と -3 の両方に掛けます。
(-4) × 2x = -8x
(-4) × (-3) = +12
よって、答えは -8x + 12 となります。

【苦手克服】分数・小数を含む計算問題
分数や小数が含まれると難しく感じますが、やることは同じです。
一つひとつ丁寧に計算しましょう。
問題1
$\frac{1}{2}$ (4a + 6)
解答・解説
分数の $\frac{1}{2}$ を 4a と +6 の両方に掛けます。
$\frac{1}{2}$ × 4a = 2a
$\frac{1}{2}$ × (+6) = +3
途中で約分を忘れないように注意しましょう。
答えは 2a + 3 です。
問題2
(10x - 15) × $\frac{1}{5}$
解答・解説
括弧の後ろに分数があってもやり方は同じです。
$\frac{1}{5}$ を 10x と -15 の両方に掛けます。
10x × $\frac{1}{5}$ = 2x
(-15) × $\frac{1}{5}$ = -3
よって、答えは 2x - 3 となります。
参考記事:中学生の数学が全くできないと悩む親へ!原因と今すぐ試せる解決策!
テストで差がつく!分配法則の応用問題
基本がマスターできたら、次は少しレベルアップした応用問題に挑戦です。
定期テストで高得点を狙うために、しっかり理解しておきましょう。
- 文字式の掛け算のルールは?
- 分数の割り算と組み合わせた問題
- 式の値を求める問題
複数の括弧を含む式の計算問題
問題
2(x + 3) + 4(x - 1)
解答・解説
このような問題では、それぞれの括弧で分配法則を使ってから、最後に同類項をまとめます。
1.前半部分の計算
2(x + 3) = 2x + 6
2.後半部分の計算
4(x - 1) = 4x - 4
3.式を合体させて同類項をまとめる
(2x + 6) + (4x - 4)
= 2x + 4x + 6 - 4
= 6x + 2
よって、答えは 6x + 2 です。

分数の割り算と組み合わせた問題
問題
(6x - 9) ÷ 3
解答・解説割り算は、逆数(ぎゃくすう)の掛け算に直すのがポイントです。
÷ 3 は × $\frac{1}{3}$ と同じです。
(6x - 9) × $\frac{1}{3}$
あとは分配法則を使います。
6x × = 2x
(-9) × $\frac{1}{3}$ = -3
よって、答えは 2x - 3 となります。

式の値を求める問題
問題
x = -2 のとき、5(x - 1) - 3(2x - 4) の値を求めなさい。
解答・解説
いきなり x = -2 を代入すると計算が複雑になります。
先に分配法則を使って式を簡単にしてから代入するのが、賢い解き方です。
1.式を簡単にする
5(x - 1) - 3(2x - 4)
= 5x - 5 - 6x + 12
= 5x - 6x - 5 + 12
= -x + 7
2.簡単にした式に x = -2 を代入する
-x + 7
= -(-2) + 7
= 2 + 7
= 9
よって、答えは 9 です。
参考記事:東大先生は怪しい!口コミ・評判の真実とは?驚きの調査結果を解説
初心者がつまずく分配法則のポイントと対策

ここでは、中1生が分配法則でやりがちなミスとその対策を紹介します。
同じ間違いを繰り返さないように、しっかり確認しておきましょう。
- 符号のミスを防ぐコツ
- 括弧の後ろの項へのかけ忘れ対策
- 分数の約分を忘れないための確認方法
符号のミスを防ぐコツ
一番多いミスが符号の間違いです。
特に「マイナス × マイナス」の計算は要注意です。
- 対策
- 声に出して確認する:「マイナス4かけるマイナス3は、プラス12」のように、声に出して計算すると、符号への意識が高まります。
- ルールを紙に書いておく:「(ー)×(ー)=(+)」「(ー)×(÷)=(ー)」のルールを机の前に貼っておくのも効果的です。

括弧の後ろの項へのかけ忘れ対策
a(b + c) の計算で、ab だけ計算して +ac を忘れてしまうミスです。
- 対策
- 矢印を書く習慣をつける:計算を始める前に、括弧の外の数から中のすべての項へ矢印を書きましょう。「全員に配る」という意識を持つことが大切です。
- 指差し確認:矢印に沿って、一つひとつ指で追いながら計算するのも確実な方法です。

分数の約分を忘れないための確認方法
分数の分配法則では、計算の途中で約分が発生します。
これを忘れると当然答えが違ってきます。
- 対策
- 計算の最後に必ず見直す:分数の計算が終わったら、「もう一度約分できないかな?」と確認する癖をつけましょう。
- 大きな分数で一気に計算しない:例えば $\frac{(4x+8)}{2}$ のような式は、$\frac{4x}{2}$+ $\frac{8}{2}$のように分けて考えると、約分忘れが減ります。
練習問題で分配法則の計算力をアップ!
分配法則のルールを理解したら、次はたくさんの問題を解いて、計算力を高めていきましょう。
- 分配法則の基礎定着ドリル
- 応用力アップ問題集
分配法則の基礎定着ドリル
まずは基本の計算問題を3問用意しました。ルールを思い出しながら解いてみましょう。
問題1 4(a + 2)
問題2 -3(x - 5)
問題3 $\frac{1}{3}$(9y + 6)
【解答・解説】
問題1 4(a + 2) = 4 × a + 4 × 2 = 4a + 8
問題2 -3(x - 5) = (-3) × x + (-3) × (-5) = (-3x) + 15 = -3x + 15
問題3 $\frac{1}{3}$(9y + 6) = $\frac{1}{3}$× 9y + $\frac{1}{3}$ × 6 = 3y + 2 = 3y + 2

応用力アップ問題集
基本がわかったら、少し複雑な応用問題に挑戦してみましょう。
テストで差がつく問題です。
問題1 5(2x - 3) - 2(x + 4)
問題2 2(4a + 1) + 3(a - 2)
問題3 (12y - 8) ÷ 4
【解答・解説】
問題1 5(2x - 3) - 2(x + 4) = (10x - 15) + (-2x - 8) = 10x - 2x - 15 - 8 = 8x - 23
問題2 2(4a + 1) + 3(a - 2) = (8a + 2) + (3a - 6) = 8a + 3a + 2 - 6 = 11a - 4
問題3 (12y - 8) ÷ 4 = (12y - 8) × $\frac{1}{4}$ = 12y × $\frac{1}{4}$ - 8 × $\frac{1}{4}$= 3y - 2 = 3y - 2
分配法則のよくある質問Q&A

最後に、分配法則に関するよくある疑問にお答えします。
- 分配法則はいつ使うの?
- なぜ(−)×(−)は(+)になるの?
分配法則はいつ使うの?
「括弧を外して式を簡単にしたいとき」に使います。
文字式の計算はもちろん、これから習う「方程式」を解くときにも必ず使います。
分配法則は、中学数学だけでなく、高校数学でも当たり前のように出てくる基本の道具なので、今のうちにしっかり身につけておくことが非常に重要です。

なぜ(−)×(−)は(+)になるの?
これは多くの人が疑問に思うポイントです。
厳密な証明は難しいですが、イメージで捉えてみましょう。
数直線を考えてみてください。
「-2を3倍する(×3)」というのは、「左に2進む動きを3回繰り返す」ことなので、-6に進みます。
では、「-2を-3倍する(×-3)」はどうでしょう?
「-3倍」を「3倍して向きを逆にする」と考えてみてください。
「左に2進む動きを3回繰り返して(-6)、その向きを逆にする」と、結果的に+6に進むことになります。
このように、マイナスを掛けることは「向きを逆にする」操作だと考えると、マイナスにマイナスを掛けると向きが元に戻ってプラスになる、とイメージしやすくなります。
※これは厳密な証明ではありませんが、イメージとして捉えるのに役立つ考え方です
オンライン家庭教師
塾より成績が上がる!オンライン家庭教師のWAM
※難関大学の講師が親切丁寧に指導!忙しい生徒にピッタリ!
短期間で成績向上!オンライン家庭教師:マナリンク
※動画でプロの講師が選べる画期的なシステム
リーズナブルな料金設定!オンライン家庭教師銀河
※中学生:1コマ30分:1,375円〜!お得に選ぶなら!銀河!
中学1年生:数学の勉強のコツ

中学1年生の数学:勉強のコツは、以下のとおりです。
基本を徹底的に理解する
中学1年生の数学は、小学校の数学と比べて難易度が上がります。そのため、基本をしっかりと理解することが大切です。教科書や問題集を繰り返し解いて、基本的な計算や公式を身につけましょう。
問題を解く力をつける
数学は、問題を解くことで身につく教科です。さまざまな問題を解いて、問題解決力を身につけましょう。教科書や問題集の例題・練習問題を繰り返し解くだけでなく、応用問題にも挑戦しましょう。
苦手分野を克服する
苦手分野があると、成績が伸び悩む原因になります。苦手分野を早めに克服するために、苦手な問題を重点的に解きましょう。また、苦手分野を克服するための参考書や問題集を活用するのもおすすめです。
定期テスト対策を万全にする
定期テストで高得点を取るためには、計画的な勉強が必要です。テスト範囲を把握して、余裕を持って勉強しましょう。また、テスト前には過去問を解いて、傾向を把握しておきましょう。
具体的な勉強方法としては、以下のようなものが挙げられます。
予習・復習を毎日行う
授業内容を予習しておくことで、授業内容を理解しやすくなります。また、授業で学んだ内容を復習することで、知識を定着させることができます。
問題を解く時間を確保する
数学は、問題を解くことで身につく教科です。毎日少しずつでも問題を解く時間を確保しましょう。
わからないことはすぐに質問する
わからないことがあると、そのまま放置してしまうと、どんどん理解が難しくなります。わからないことはすぐに質問して、理解を深めましょう。
中学1年生の数学は、数学の基礎を学ぶ大切な時期です。
基本をしっかりと理解して、問題を解く力を身につけて、数学が好きになるようにしましょう。
おすすめ塾
塾よりも成績が上がる!
東大生など、有名大学やプロ講師
安心の成績保証制度!
学校の勉強から超難関受験対策
まとめ:中1数学の分配法則問題集!文字式の計算をマスター

今回は、中学1年生の数学でつまずきやすい「分配法則」について、基本的な使い方から応用問題、ミスの防ぎ方まで詳しく解説しました。
最後に、この記事の重要なポイントを振り返りましょう。
中1の数学を攻略!分配法則のポイント
ポイント
- 分配法則の基本
括弧の外の数を、中のすべての項に公平に掛けること。 - 計算のコツ
矢印を書いてかけ忘れを防ぎ、符号のルールを意識すること。 - 応用問題の解き方
割り算は逆数の掛け算に直し、式の値は先に式を簡単にしてから代入すること。 - 練習が一番の近道
たくさんの問題を解いて、計算のスピードと正確さを上げること。
分配法則は、練習すれば必ず得意にできる単元です。
練習問題を繰り返し解いて、自信を持ってテストに臨めるように頑張ってください!
数学の勉強法一覧
数学の勉強法を紹介しています。
参考にしてください。

