
※この記事には一部PRが含まれます。
「割合が始まった途端、子どもが算数嫌いになってしまった……」と悩むお母さま、
安心してください。
割合は、5年生の算数で最もつまずきやすい難所ですが、教え方のコツさえ掴めば必ず分かります。
27年の指導経験から、公式を丸暗記せずに「一生迷わなくなる考え方」を、今日から使える言葉でお伝えします。
記事のポイント
「割合」を「何倍か」という言葉に置き換える
「〜の」の直前にある「基準(もとの量)」を探す
公式よりも先に「かけ算の形」で式を作る
「100%=1」という単位変換のルールを固める
タブレット教材
Contents
わかりやすく!小学生の「割合とは?」つまずくのは普通のこと

割合の授業が始まってお子さんが混乱していても、それは決して能力のせいではありません。
これまでの算数とは「考え方のルール」が少し変わるため、戸惑うのはごく自然なことです。
まずは、なぜ多くの子がここで立ち止まってしまうのか、その理由を知ることから始めましょう。
- 「どっちで割るの?」と迷ってしまう理由
- 親が説明しづらいと感じるポイント
「どっちで割るの?」と迷ってしまう理由
お子さんが一番苦労するのは「どっちの数字を、どっちで割るか判断できない」という点です。
これは、文章題に出てくる数字を、意味を考えずに公式に当てはめようとしているからです。
特に「8は40の何倍?」のように、小さい数を大きい数で割る問題が出ると、「割り算=答えが小さくなるはず」という今までの常識が通用しなくなり、パニックになってしまいます。
計算ができないのではなく、新しい数(1より小さい数)のルールに戸惑っているだけなのです。

親が説明しづらいと感じるポイント
「もとにする量」や「比べられる量」といった言葉が、日常で使わない難しい言葉であることが最大の壁です。
- 言葉自体が堅苦しくてイメージしにくい
- 「公式を覚えなさい」と言っても、問題が少し変わると解けなくなる
- 自分が教えると、つい熱くなって親子でケンカになってしまう
塾の現場でも、多くの保護者さまが同じ悩みを抱えています。
教えるのが難しいのは、お母さまの教え方のせいではなく、教科書の言葉が難しすぎるから。まずはそのプレッシャーを手放してください。
割合とは何かを簡単に説明すると

割合を一言で言うなら、それは「何倍かな?」という言葉の言い換えです。
難しく考えがちな「割合」という言葉の正体を、お子さんの目線に合わせて噛み砕いてみましょう。
小学校の算数で本当に理解すべき核心部分は、実はとてもシンプルです。
- 割合の意味をやさしい言葉で理解しよう
- 小学校の算数で習う「割合」とは
割合の意味をやさしい言葉で理解しよう
お子さんに教えるときは、難しい定義ではなく「割合=何倍のことだよ」と伝えてあげてください。
これが最も本質的で、お子さんが安心できる説明です。
例えば、お菓子が2個あって、お母さんが10個持っていたら「お母さんは私の5倍だね」と言います。
この「5倍」という数字そのものが割合です。
「倍」という言葉なら低学年から慣れ親しんでいるため、お子さんも「なんだ、そういうことか!」と納得しやすくなります。
「何倍かを数字で表すのが割合なんだよ」と教えてあげてください。
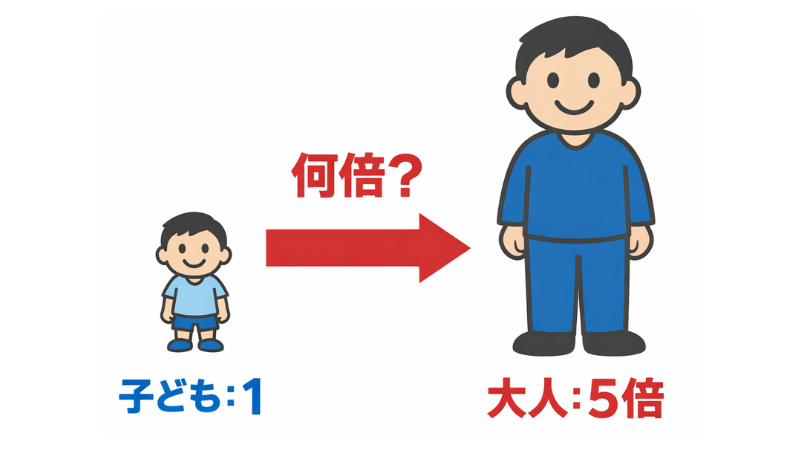
小学校の算数で習う「割合」とは
学校での学習は、「基準を『1』に決める」という世界共通のルールを学ぶ時間です。
これを整理すると、以下のようになります。
| 学校の言葉 | わかりやすい言い換え |
|---|---|
| もとにする量 | 基準となる「1」の大きさ |
| 比べられる量 | 知りたい方の大きさ |
| 割合 | 「何倍か」を表す数 |
このように、割合とは単なる計算ではなく、「2つの数字の関係を比べるための道具」なのです。
割合は「くらべる」考え方

割合で最も大切なのは、計算の前に「何を基準に比べているのか」をハッキリさせることです。
どれが基準(100%)なのかを見極める力を養うことで、立式で迷うことはなくなります。
- どれがもとになる数かを見つける
- 「どれが100%か」を先に考える
どれがもとになる数かを見つける
文章題を読んだときに、真っ先に探すべきなのが「基準(もとにする量)」です。これさえ見つかれば、問題の半分は解けたも同然です。
塾で教えている最も簡単な見つけ方は、「〜の」の直前にある言葉に注目することです。
- 「弟の体重の0.8倍」→基準は「弟」
- 「定価の2割引き」→基準は「定価」
このように、「『〜の』の前にいるのがリーダー(基準の1)だよ」と教えてあげてください。
これだけで、迷子がぐっと減ります。

「どれが100%か」を先に考える
割合を考えるとき、私はいつも生徒に「どれを『1(100%)』にする?」と問いかけます。
例えば、クラス全体を100%としたとき、女子が40%なら男子は60%。このように、基準となる「全体」をしっかり「1」や「100%」と固定することで、数の大きさが直感的にイメージできるようになります。
この感覚さえ掴めれば、算数のセンスは一気に磨かれます。

割合とパーセントの関係をわかりやすく整理
割合には「0.2」のような小数のほかに、「20%」や「2割」といった呼び方があり、これが混乱の元です。
これらは「同じものの別の名前」にすぎません。一目でわかる対応表で整理しましょう。
- 割合とパーセントの違いと共通点
- 小学生が混乱しやすいポイント
割合とパーセントの違いと共通点
割合は「1」を基準にしますが、パーセント(百分率)は「100」を基準にします。
これは、細かい数字を私たちの生活で使いやすくするための工夫です。
| 小数(割合) | パーセント(百分率) | 歩合(割・分・厘) |
|---|---|---|
| 1 | 100% | 10割 |
| 0.1 | 10% | 1割 |
| 0.01 | 1% | 1分 |
呼び方は違っても、表している「大きさ」は全く同じです。
「1=100%=10割」という横の繋がりをセットで見る習慣をつけるのが、苦手克服の近道です。
小学生が混乱しやすいポイント
多くの子が「1%=0.1」だと思い込むミスをします。正しくは「1%=0.01」ですが、ここでの桁間違いが失点の原因です。
特に「0.1%」のような小さな数字や、「120%」といった1を超える数字で混乱します。
「100%が基準の『1』」というルールを繰り返し確認し、「%から小数に直すときは、点を左に2つ動かすんだよ」と具体的に教えてあげると、ミスは劇的に減ります。
割合の求め方はこの考え方で迷わない

「かけるのか、割るのか」という迷いを消すには、公式をバラバラに覚えるのをやめることです。
たった一つの「かけ算の形」をベースにするだけで、どんな問題も解けるようになります。
- 割るか掛けるかを判断する順番
- 文章問題で考えるときのコツ
割るか掛けるかを判断する順番
いきなり割り算で考えず、まずは「もとにする量 × 割合 = 比べられる量」というかけ算の形に当てはめてみましょう。
「AのB倍はC」という形に整理するだけです。
もし「倍(割合)」がわからないなら「A × □ = C」となります。
この「逆算の形」を作ってから、最後に割り算をするという手順を踏むことで、計算順序の間違いはなくなります。
「最初の式は必ずかけ算で作る」。これが最も安全な解き方です。
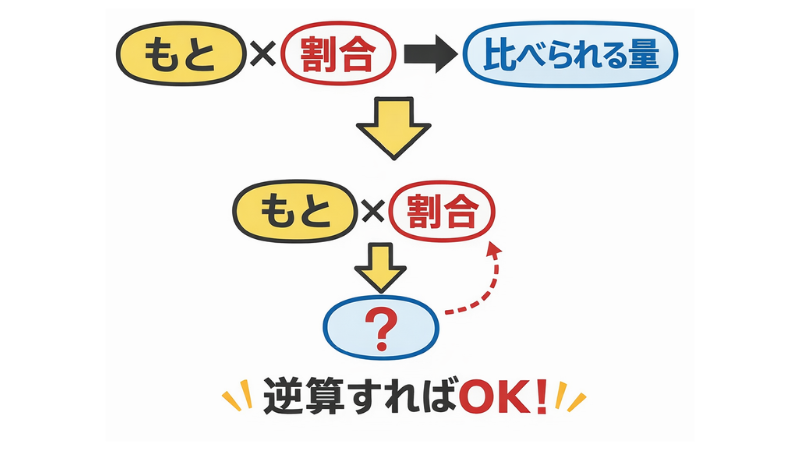
文章問題で考えるときのコツ
数字だけで考えようとせず、「数直線」をかく習慣をつけましょう。
- 横棒を一本引く
- 「もと」の数字を上に、その割合(1)を下に書く
- 「比べられる」数字を上に、その割合を下に書く
視覚化すると、「どの数字同士がセットか」が一目でわかります。
「図は式を教えてくれる地図だよ」と伝えて、まずは落書き感覚で図を書かせてあげてください。

例題で割合の考え方を確認しよう

ここまでの内容を、実際の例題で確認しましょう。
大切なのは計算の速さではなく、考え方のステップが正しいかどうかです。
- 割合を求める基本の例
- 数を求める文章問題の例
割合を求める基本の例
【問題】40人のクラスのうち、メガネをかけている人は10人です。メガネの人はクラス全体の何%ですか?
まず基準を探します。「全体の」とあるので、40人が基準の「1」です。
これを「かけ算の形」にすると、「40 × □ = 10」。
□を出すために「10 ÷ 40」をして「0.25」。
パーセントに直して「25%」が正解です。「全体に対してどれくらいか」を出すのが割合の基本です。
数を求める文章問題の例
【問題】定価2,000円のゲームが30%引きで売られています。安くなった金額は何円ですか?
「定価の」とあるので、2,000円が基準(もと)です。
30%は「0.3倍」のことなので、「2,000 × 0.3 = □」。
計算すると「600」、答えは「600円」です。
「30%は0.3倍のこと」とパッと変換できる力があれば、お買い物も楽しくなります。
小学5年生で割合を学ぶときの注意点

5年生の算数で、割合は最大の山場です。なぜ難しく感じるのか、その正体を知っておくだけで、フォローの仕方が変わります。
- 4年生までの算数とのつながり
- 5年生で割合が難しく感じる理由
4年生までの算数とのつながり
割合の基礎は、2年生の「かけ算」や「○倍」から始まっています。
そして4年生で「小数」を学びました。
5年生の割合は、これらを合体させて使う単元です。
「12÷4=3」という計算が「12は4の3倍である」という意味を持つことを、これまでどれだけ意識できていたかが鍵となります。
苦戦しているなら、「割り算の意味」まで少し戻ってあげることが、実は一番の近道です。
5年生で割合が難しく感じる理由
最大の理由は、「計算すると数字が小さくなる」という、今までの常識がひっくり返る体験をするからです。
- 「0.8倍」すると、元の数より小さくなる
- 「0.5で割る」と、元の数より大きくなる
この現象が不思議で、「自分の式が間違っているかも」と不安になるのです。
「1より小さい数をかけると小さくなる。これは新しいルールなんだよ」と、お子さんの不安を肯定してあげてください。
親が子どもに伝えるときの声かけ例

家庭で教える際、お子さんの自信を奪わずに理解を助ける「魔法のフレーズ」をご紹介します。
- そのまま使える説明フレーズ
- 子どもが安心する言い方
そのまま使える説明フレーズ
お子さんが迷ったときは、こう声をかけてみてください。
- 「『割合』って言葉を、『何倍かな?』に変えて読んでごらん」
- 「文章の中にある『〜の』の前の言葉に丸をつけてみよう」
- 「計算は後でいいから、どっちが基準の『1』かな?」
一度にすべて教えようとせず、ステップを分けるのがコツです。
「基準さえ見つかればOK!」と、ハードルを下げてあげましょう。

子どもが安心する言い方
「お母さんも昔、ここで苦労したんだよ」という共感は、最高の薬です。
「この単元は大人でも間違えるくらい難しいから、今わからなくても大丈夫」と伝えてください。
点数よりも、「図を書こうとしたこと」「基準を探そうとしたこと」を具体的に褒めましょう。
お母さまの「焦らない姿勢」が、お子さんの理解を一番助けます。
【専門家からのアドバイス】
割合は、教え方ひとつでお子さんが算数嫌いになるか、得意になるかが分かれるデリケートな単元です。「どうしても親子だと感情的になってしまう」「プロの視点で基礎から立て直してほしい」という場合は、無理に家庭だけで抱え込む必要はありません。
最近では、算数特化の指導や、割合のつまずきをピンポイントで解消してくれるオンラインサービスも充実しています。
▶小学生向けオンライン家庭教師おすすめ比較|料金・講師・体験で選ぶ総合ランキング
【Q&A】小学生の割合とは?についてよくある質問
保護者さまからよくいただく疑問にお答えします。
- Q.割合とは簡単に言うとどういう意味ですか?
- Q.割合とパーセントはどう違うのですか?
- Q.割合は小学校の何年生で習いますか?
- Q.割合は算数の中で何が一番大切ですか?
Q.割合とは簡単に言うとどういう意味ですか?
一言で言うと「ある量を『1』としたとき、もう一方がその何倍にあたるか」を表した数です。
「大きさを比べるための物差し」だと捉えてください。

Q.割合とパーセントはどう違うのですか?
ルールの違いだけです。割合は「1」を基準にし、パーセントは「100」を基準にします。
「0.2」をわかりやすく100倍して「20%」と呼んでいるだけで、中身は同じです。

Q.割合は小学校の何年生で習いますか?
主に小学5年生で習います。4年生で準備をし、6年生の「比」へと繋がっていく、算数の中で最も重要な土台となる時期です。

Q.割合は算数の中で何が一番大切ですか?
「基準(もとにする量)を正しく見極めること」です。計算は電卓でもできますが、「何を1とするか」の判断は人間にしかできません。
この力は、将来ニュースやデータを読み解く際にも役立つ「一生モノの武器」になります。
東大生家庭教師
現役の東大生が指導するオンライン家庭教師!
当サイト人気ランキングTOP3
第1位:東大生によるオンライン個別指導トウコベ
※講師のほとんどが現役東大生!しかも、圧倒的な低価格を実現!安心の返金保証制度で生徒の成績アップをサポートします。
第2位:オンライン家庭教師「東大先生」
※当サイトで人気の東大生によるオンライン家庭教師!講師全員が現役東大生・東大院生!資料請求で勉強が変わること間違いなし!
第3位:オンライン東大家庭教師友の会
※東大生をはじめとする難関大生がマンツーマンでオンライン指導!講師の2人に一人が厳しい採用基準を突破した現役東大生!
まとめ:割合とは?小学生にわかりやすく求め方を解説「どっちで割る?」か迷わない

割合は公式より考え方が大切
公式を丸暗記しても、意味を忘れてしまえば使えません。
それよりも、「何倍かな?」と考える癖や、図を書いて整理する力を育むことの方が、ずっとお子さんのためになります。
主役は公式ではなく、「文章を読み解く力」であることを忘れないでください。
次につながる算数の学び
割合をマスターすると、その後の「比」や「速さ」、中学の「方程式」もスムーズになります。
焦らず、今回ご紹介した「かけ算ベースの考え方」を試してみてください。
塾オンラインドットコム編集部は、専門家の知見を活かし、皆さんの家庭学習を心から応援しています。
執筆者のプロフィール
【執筆者プロフィール】

塾オンラインドットコム【編集部情報】
塾オンラインドットコム編集部は、教育業界や学習塾の専門家集団です。27年以上学習塾に携わった経験者、800以上の教室を調査したアナリスト、オンライン学習塾の運営経験者、ファイナンシャルプランナー、受験メンタルトレーナー、進路アドバイザーなど、多彩な専門家で構成されています。小学生・中学生・受験生・保護者の方々が抱える塾選びや勉強の悩みを解決するため、専門的な視点から役立つ情報を発信しています。
塾オンラインドットコム:公式サイト、公式Instagram


